Enigma Virtual Box unpacker
There are plenty of changes.
- Properly detect versions 9.50..9.90
- Unpacks files packed with 9.80 and 9.90
- Added command-line parameter "/nodiskspace", as requested by some users. If it crashes during unpacking because it ran out of disk space, it's your problem.
- Unpacker properly handles invalid input filename
Molebox 2.x unpacker
- Support more versions of very old Molebox
- Unpacking files with digital signatures should be improved
- Some rare bugs have been fixed
Autoplay Media Studio unpacker
- Added support for AMS version 8.5.3.0.
- Support for Imagine MemoryEx encrypted files, as requested by someone.
What is MemoryEx?
MemoryEx is a plugin released by Imagine Programming, allowing for more advanced operations from within the Lua environment you will find in Autoplay Media Studio 8.
While it's not a very common plugin, there are several niche programs which use this plugin. For example, most programs from dindroid.com use it.
When you unpack such file, please pay attention to the "Found protected file" messages:
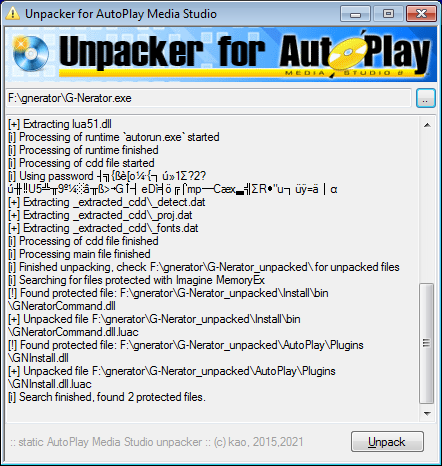
As you can see, unpacker created some .luac files.
Next, you will need to find a LUA decompiler and decompile these files. I suggest you try unluac, luadec or whichever LUA decompiler you prefer.
Decompiler should produce .lua file which contains all the interesting stuff. For example, part of G-Nerator code looks like this:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
return { info = { name = "Anderson M Santos", author = "dindroid.com", contact = "andersonnsantos36@gmail.com" }, functions = { Install = function() function Stile_Sonbre_P() sHandl = Application.GetWndHandle() DLL.CallFunction(_SystemFolder .. "\\User32.dll", "SetClassLongA", sHandl .. ",-26," .. 131072, DLL_RETURN_TYPE_LONG, DLL_CALL_STDCALL) if Label.GetText("local") == "C:\\" then Label.SetText("local", _ProgramFilesFolder .. "\\Dindroid") end Image.Load("imico", _TempFolder .. "\\icon.tmp") Image.Load("imc", _TempFolder .. "\\bts_01.tmp") end function Install() Folder.Create(_ProgramFilesFolder .. "\\Dindroid" .. "\\G-Nerator") File.Copy(_SourceFolder .. "\\Install\\*.*", _ProgramFilesFolder .. "\\Dindroid" .. "\\G-Nerator", true, true, false, true, nil) sP = System.EnumerateProcesses() for j, file_path in pairs(sP) do file = String.SplitPath(file_path) if file.Filename .. file.Extension == "GNerator.exe" then File.Copy(file_path, _ProgramFilesFolder .. "\\Dindroid" .. "\\G-Nerator\\") end end Shell.CreateShortcut(String.Replace(_WindowsFolder, "Windows", "") .. "\\Users\\Public\\Desktop", "G-Nerator", _ProgramFilesFolder .. "\\Dindroid" .. "\\G-Nerator\\GN.exe", "", "", _ProgramFilesFolder .. "\\Dindroid\\G-Nerator\\GN.exe", 0, SW_SHOWNORMAL, nil, "") .... |
That's all folks, have fun using it!
As always - if you notice any bugs, please report them. And most importantly - Happy New Year everybody! smile


