Enigma’s EP_CryptDecryptBuffer internals
For one of my private projects, I needed to decrypt some data. Original executable uses Enigma's EP_CryptDecryptBuffer function but I needed to implement the same thing using .NET. Much to my surprise, there was no information about what encryption algorithm is used by Enigma or how it works internally. So, I started by compiling Enigma's sample project CryptBuffer and debugging the executable.
TL;DR - IDEA cipher in CBC mode, password = MD5(user_password), IV for CBC comes from IDEA.Encrypt(8-zeroes, password).
Research
After protecting my executable with Enigma, few assembly lines
|
1 2 3 4 |
004142FA 68 B85E4100 PUSH crypto_p.00415EB8 ; ASCII "password" 004142FF 68 00100000 PUSH 1000 00414304 53 PUSH EBX 00414305 E8 EEF9FFFF CALL <JMP.&enigma_ide.EP_CryptDecryptBuf> |
got changed into something horrible that looked like an Enigma's VM:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
004142FA 68 B85E4100 PUSH crypto_p.00415EB8 ; ASCII "password" 004142FF 68 00100000 PUSH 1000 00414304 53 PUSH EBX 00414305 E8 EEF9FFFF CALL crypto_p.00413CF8 .. 00413CF8 FF25 44D44100 JMP DWORD PTR DS:[41D444] ; crypto_p.004EEC6C .. 004EEC6C /E9 C6A60800 JMP crypto_p.00579337 .. 00579337 68 6D5133A1 PUSH A133516D 0057933C E9 BBC1FEFF JMP crypto_p.005654FC .. 005654FC 60 PUSHAD 005654FD 9C PUSHFD 005654FE B2 01 MOV DL,1 00565500 BE 00000000 MOV ESI,0 00565505 8DBE CC775600 LEA EDI,DWORD PTR DS:[ESI+5677CC] 0056550B 8D3F LEA EDI,DWORD PTR DS:[EDI] 0056550D B9 01000000 MOV ECX,1 00565512 31C0 XOR EAX,EAX 00565514 F0:0FB10F LOCK CMPXCHG DWORD PTR DS:[EDI],ECX ; LOCK prefix 00565518 74 0F JE SHORT crypto_p.00565529 0056551A 3A15 C8775600 CMP DL,BYTE PTR DS:[5677C8] ... |
I didn't feel like spending my time on analyzing that. Much easier solution was to put hardware breakpoints on my data and password and wait for them to trigger. In a few seconds I landed into code that looked like MD5 (notice the constants!):
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
... 00454E1C 89D7 MOV EDI,EDX 00454E1E 31CF XOR EDI,ECX 00454E20 21DF AND EDI,EBX 00454E22 31D7 XOR EDI,EDX 00454E24 01F0 ADD EAX,ESI 00454E26 8D8407 78A46AD7 LEA EAX,DWORD PTR DS:[EDI+EAX+D76AA478] 00454E2D C1C8 19 ROR EAX,19 00454E30 01D8 ADD EAX,EBX 00454E32 8B75 04 MOV ESI,DWORD PTR SS:[EBP+4] 00454E35 89CF MOV EDI,ECX 00454E37 31DF XOR EDI,EBX 00454E39 21C7 AND EDI,EAX 00454E3B 31CF XOR EDI,ECX 00454E3D 01F2 ADD EDX,ESI 00454E3F 8D9417 56B7C7E8 LEA EDX,DWORD PTR DS:[EDI+EDX+E8C7B756] ... |
and few hits later I landed into code that I didn't recognize at first:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
... 004DB61C E8 DBFDFFFF CALL crypto_p.004DB3FC 004DB621 66:8B446E 7E MOV AX,WORD PTR DS:[ESI+EBP*2+7E] 004DB626 66:0147 02 ADD WORD PTR DS:[EDI+2],AX 004DB62A 66:8B846E 800000>MOV AX,WORD PTR DS:[ESI+EBP*2+80] 004DB632 66:0147 04 ADD WORD PTR DS:[EDI+4],AX 004DB636 66:8B946E 820000>MOV DX,WORD PTR DS:[ESI+EBP*2+82] 004DB63E 8D47 06 LEA EAX,DWORD PTR DS:[EDI+6] 004DB641 E8 B6FDFFFF CALL crypto_p.004DB3FC 004DB646 66:8B47 04 MOV AX,WORD PTR DS:[EDI+4] 004DB64A 66:894424 0C MOV WORD PTR SS:[ESP+C],AX 004DB64F 66:8B07 MOV AX,WORD PTR DS:[EDI] 004DB652 66:3147 04 XOR WORD PTR DS:[EDI+4],AX ... |
Delphi compiler had helpfully included RTTI information telling me that this second piece of code belongs to a class called TIdeaCipher. Now I had all the information I needed, I just had to put it all together. smile
Implementing decryption in C#
There aren't many IDEA implementations in C#. In fact, there are 2: by BouncyCastle and by LexBritvin. Since I'm not a big fan of huge and complex libraries like BouncyCastle, so I took the simplest possible code: from Github and modified it a bit.
First, we need change password generation algorithm to use MD5 to generate real password:
|
1 2 3 4 5 |
private static byte[] generateUserKeyFromCharKey(String charKey) { MD5 md5 = MD5.Create(); return md5.ComputeHash(Encoding.ASCII.GetBytes(charKey)); } |
Second, we need to add support for CBC mode. It requires both calculating correct IV value and pre/post-processing each block we're encrypting or decrypting.
Calculating IV is quite simple:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
// IV for CBC mode byte[] IV; public Idea(String charKey, bool encrypt) { byte[] key = generateUserKeyFromCharKey(charKey); // Expands a 16-byte user key to the internal encryption sub-keys. int[] tempSubKey = expandUserKey(key); // calculate IV subKey = tempSubKey; IV = new byte[8]; crypt(IV, 0); if (encrypt) { subKey = tempSubKey; } else { subKey = invertSubKey(tempSubKey); } } |
Processing each block is slightly harder but not a rocket science either. As explained in image borrowed from Wikipedia:
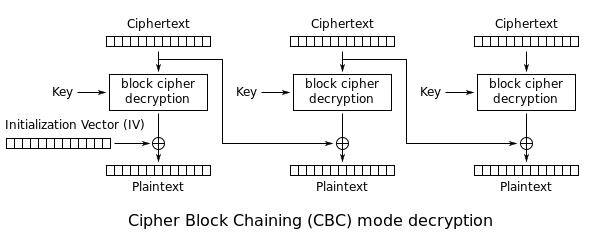 .
.
Before decrypting the data block, we need to store the encrypted values as IV for the next block. After decrypting the block, we need to XOR each byte of data with a corresponding byte of IV. Unfortunately, during encryption the data flow is different, so the simple crypt function has to be replaced with 2 functions: encrypt and decrypt.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
/** * Decrypts array * * @param data * Buffer containing data bytes to be decrypted */ public void decrypt(byte[] data) { for (int q = 0; q < data.Length; q += 8) { // save original bytes for next IV byte[] origBytes = new byte[8]; Array.Copy(data, q, origBytes, 0, 8); // decrypt data crypt(data, q); // xor data with previous IV for (int w = 0; w < 8; w++) data[q + w] ^= IV[w]; // copy original data to next IV Array.Copy(origBytes, IV, 8); } } |
Few more cosmetic changes and that's it! We got clean and nice implementation of EP_CryptDecryptBuffer in pure C#. smile
Download link: https://bitbucket.org/kao/ep_cryptdecryptbuffer/
Have fun!
P.S. My implementation only supports cases where data length is divisible by 8, adding support for other lengths is left as an exercise for the reader.